TANGENTIAL GLISSETTE
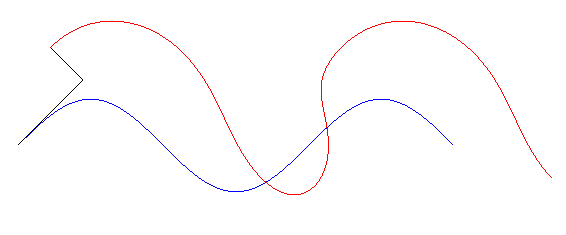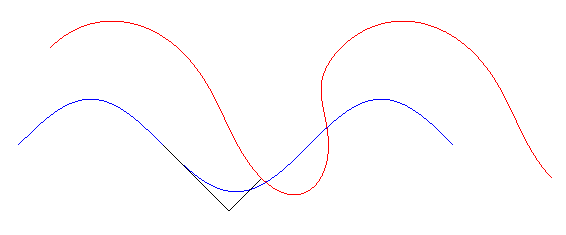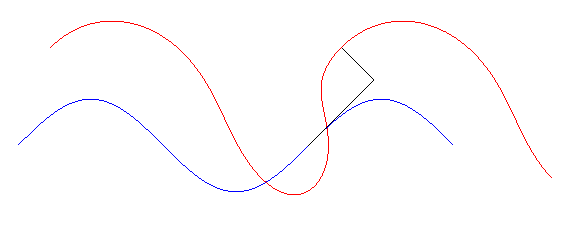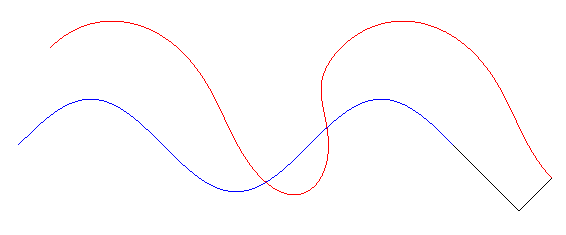
Tangential glissette of a sinusoid
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TANGENTIAL GLISSETTE

Tangential glissette of a sinusoid
| Cartesian parameterization for a glissette of X,
Y coordinates in the Frenet coordinate system, the starting curve being
parameterized by |
The tangential glissettes
of a curve (C) are the traces in the fixed plane of the points of
a plane related to a sliding tangent on the curve
(C); see glissette
(case # 1 dual). In other words, these are the trajectories of the points
having fixed coordinates in the Frenet coordinate system moving along the
curve.
The normal line to the curve rolling without sliding on the evolute, the tangential glissettes are the roulettes of the movement "plane over plane" of base curve the evolute and rolling curve the normal line.
When the tracer point is on the tangent, the glissettes are the equitangential curves associated with (C), and when it is on the normal line, the glissettes are none other than the curves parallel to (C).
SPECIAL CASE OF EQUITANGENTIAL CURVES (Y=0,
X=d)
| Cartesian paramétrization: |
Exemple of the ellipse :
| Cartesian paramétrization: Note that according to Holditch's theorem, the area swept by the tangent segment is |
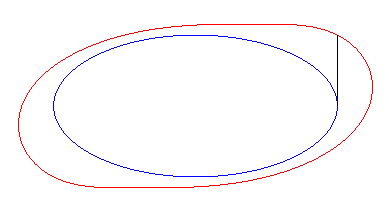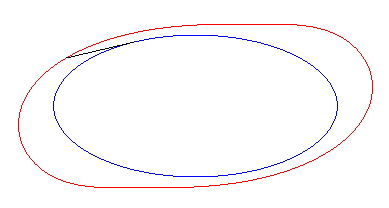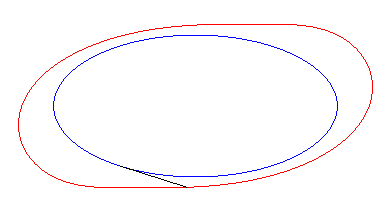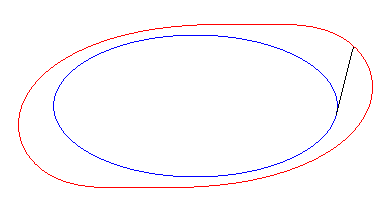 |
| The starting curve is a tractory
of its equitangential curves.
So, more concretely, the equitangential curves are the curves of the front wheels of bicycles which one imposes on the rear wheel to follow the starting curve. |
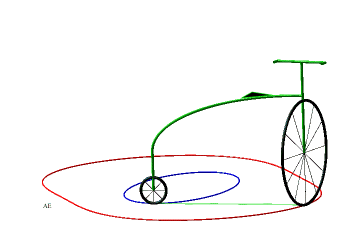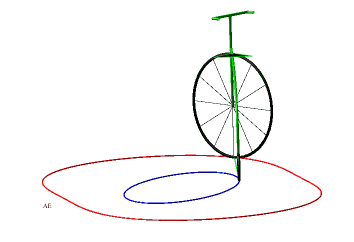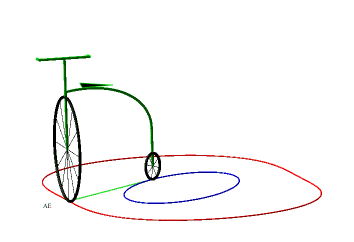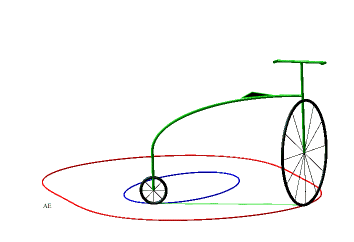 |
Below, case of the cycloïde
and Bernoulli lemniscate.
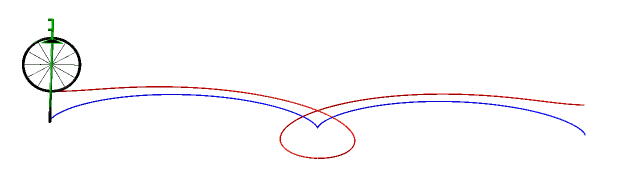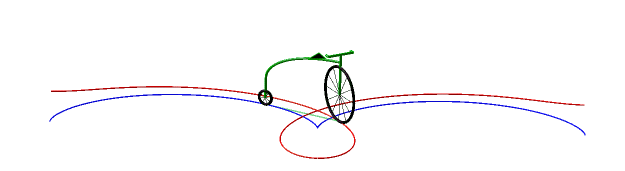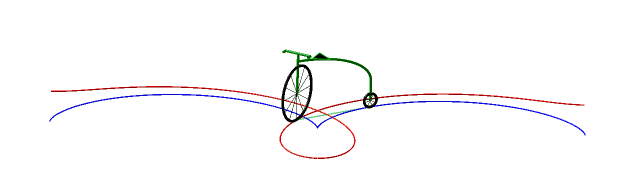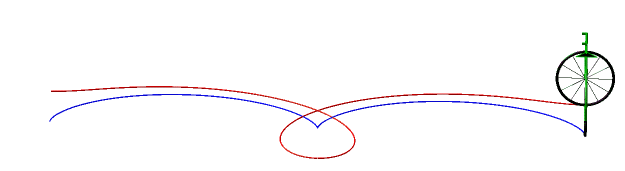 |
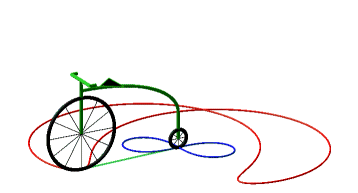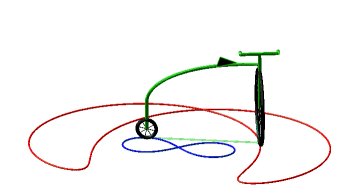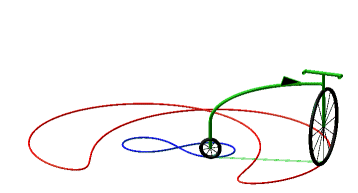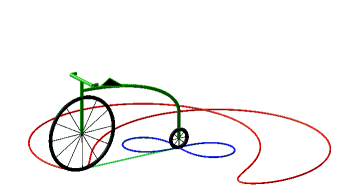 |
See the syntractrixes,
equitangential curves of the tractrix.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2019